On This Page
Sun 20 Mar 2016
Find kth largest element in an array
Tags: algorithm ruby heap max-heap projects
The other day I stumble upon the question to find the kth largest element in the array. At first glance, I thought the solution was trivial. But later I thought that there are multiple ways to achieve efficient solution
Heap is a useful data structure when root of the tree is important. Extracting an element from the heap is in logarithmic time. This could be used to find kth element from the array since finding maximum or minimum in heap is constant time.
Problem Statement
Suppose, we have an array of arbitrary integer values. We need to find the kth largest element in the array. A sample of the input file is given below
3
9, 4, 5, 2, 1, 23, 55, 88, 74
Here, the first line is the value of n and next line contains the array
Desired Output
The output should print the 3rd element in the array i.e.
55
Step 1 aka Read the input file
Before we begin, we need to perpare our tools and gather required inputs. First we need to read the input file and get the value of k and the array. Also I’ll be using ruby to write code as it is closer to psuedo code. So fire up your text editor and paste the code below
| filename = 'input.txt' | |
| #Read the file | |
| txt = File.open(filename, 'r') | |
| #get the first value | |
| n_value = txt.first | |
| #read the next line and split the line based on comma | |
| #and save it in array | |
| array_value = txt.first.split(',') | |
| txt.close |
Step 2 aka the easy way
One of the first solution that pops in my mind to find the nth largest element is
- Sort the array in descending order
- Get the element at the kth index
The time complexity for this solution is @L O(n\log{}n) @L . However we can still find another solution in @L O(n) @L time.
More Efficiently?
We can visualize our array as tree with each value as a node of tree. However to build our array as heap , we need to satisfy certain properties
- Each node of the heap has value
- Value of each node @L \ge @L values of each of its children (Max-heap)
In a nutshell our array should look like this
88,74,23,55,1,5,9,2,4
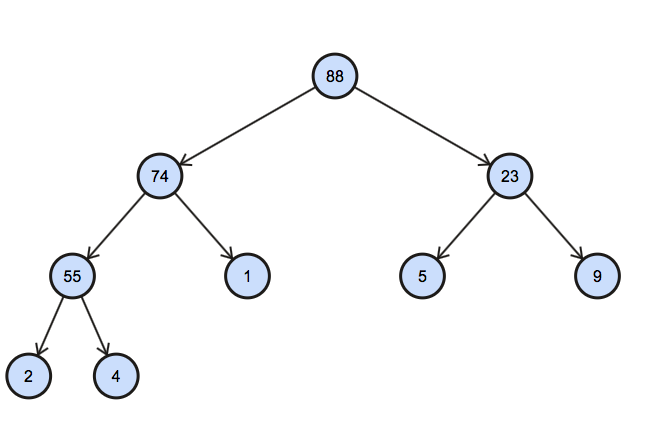
Building the heap
Building heap takes O(n) time. First visit to every non-leaf node and checks if the value at the node satisfy heap property.
| # build heap | |
| # time O(n) time | |
| def build_heap(nums) | |
| nums_size = nums.length | |
| # get all the non-leaf nodes | |
| i = (nums_size / 2) - 1 | |
| while i >= 0 | |
| #heapify it | |
| max_down(nums, i, nums.length) | |
| i = i - 1 | |
| end | |
| end | |
Max_down() is the most important function as it heapifies (or maintain the heap property).
| # Maxheap | |
| def max_down(nums, i, nums_size) | |
| #debug = '' | |
| # check if the root element is greater than | |
| # left-most leaf | |
| if (2 * i + 1) < nums_size and nums[2 * i + 1] > nums[i] | |
| largest = 2 * i + 1 | |
| else | |
| largest = i | |
| end | |
| # check if the largest element is greater than | |
| # rightmost leaf | |
| if (2*i +2) < nums_size and nums[2 * i + 2] > nums[largest] | |
| largest = 2 * i + 2 | |
| end | |
| if defined? debug | |
| puts("i is " + i.to_s + " and A[i] is " + nums[i].to_s + " and largest is " + largest.to_s + " and A[largest] is " + nums[largest].to_s) | |
| end | |
| #if the root element needs to change | |
| # to statisfy the heap quality | |
| if i != largest | |
| #swap element | |
| swap_variable = nums[i] | |
| nums[i] = nums[largest] | |
| nums[largest] = swap_variable | |
| max_down(nums, largest, nums_size - 1) | |
| end | |
| end |
Extract Max
Our last step involves extracting the kth max element.
- Extract the fist element which is the root element @L O(1) @L
- Call heapify to maintain heap property @L O(\log{}(n) @L
- Call extract k times extract max @L O(k \log{}(n)) @L
| # get the leargest element | |
| # and heapify it | |
| # nums is the input array | |
| # nums_size is the length of the input array | |
| def extract_max(nums, nums_size) | |
| elem = nums[0] | |
| nums[0] = nums[nums_size - 1] | |
| # now the size reduces by 1 | |
| # heapify it | |
| max_down(nums, 0, nums_size - 1) | |
| return elem | |
| end | |
| # nums is the input array | |
| # k is the k^th largest elment in array | |
| def k_largest(nums, k) | |
| #building a heap and inserting array's elements into heap | |
| build_heap(nums) | |
| #get the largest element | |
| nums_size = nums.length | |
| i = 0 | |
| while i < k | |
| elem_max = extract_max(nums, nums_size) | |
| nums_size = nums_size - 1 | |
| i = i + 1 | |
| end | |
| return elem_max | |
| end |
Conclusion
Time complexity analysis of two methods discussed above
| Using | Worst Case | Description |
| Sort | O(n log(n)) + O(1) | Sorting the array + accessing the element |
| Heap | O(n) + O(k log(n)) | Building heap + extracting maximum element |